Function Values Of Special Angles

Trigonometric Special Angles – Caption & Examples

We normally need to use the calculator to figure out the values of the trigonometric functions of an angle unless nosotros are dealing with trigonometric special angles. Because it is non possible to precisely evaluate the trigonometric functions for most of the angles. Merely is it true for all the angles? The answer is no — not always.

Trigonometric special angles — 30^o, 45^o, and sixty^o— generate rather straightforward trigonometric values. Nosotros can precisely evaluate the trigonometric functions for these special angles without a estimator.

Subsequently studying this lesson, we are expected to acquire the concepts driven by these questions and be qualified to accost accurate, specific, and consistent answers to these questions.

What are trigonometric special angles?
How to solve trigonometric special angles?
How tin can we solve actual problems using trigonometric special angles?

The goal of this lesson is to clear up any confusion you might have about the concepts involving trigonometric special angles.

What are trigonometric special angles?

At that place are specific angles that provide simple and verbal trigonometric values. These specific angles are known as trigonometric special angles. These are 30^o, 45^o, and 60^o .

What is so special about them?

Because it is piece of cake to 'exactly' evaluate the trigonometric function without using a calculator for these angles. These angles have comparatively clean values, offering us a great deal to solve Math bug. We apply these values to give precise answers for determining the values of many trigonometric ratios.

We will use 2 'special right triangles' to discuss the special angels in this lesson.

45^o – 45^o – xc^o triangle — also known every bit isosceles triangle — is a special triangle with the angles 45^o, 45^o, and 90^o.
30^o – 60^o – 90^o triangle is some other special triangle with the angles xxx^o, 60^o, and 90^o.

These special triangles take a unique ability to provide us precise and simple answers when dealing with trigonometric functions.

The skillful thing is that you are already familiarized with these special triangles as we have discussed them in our Geometry lessons. Nosotros will just use them to solve trigonometric special angles and determine the trigonometric ratios of these special angles.

How to solve trigonometric special angles?

Case one:

Special angle 45^o (from a 45^o – 45^o – 90^o triangle)

The following figure 7-1 represents a $45^{\circ }$ – $45^{\circ }$ – $ninety^{\circ }$ isosceles right triangle with two $45^{\circ }$ caste angles. The lengths of the 3 legs of the right triangle are named $a$, $b$, and $c$. The angles opposite the legs of lengths $a$, $b$, and $c$ are named $A$, $B$, and $C$. The tiny square with the bending $C$ shows that information technology is a right angle.

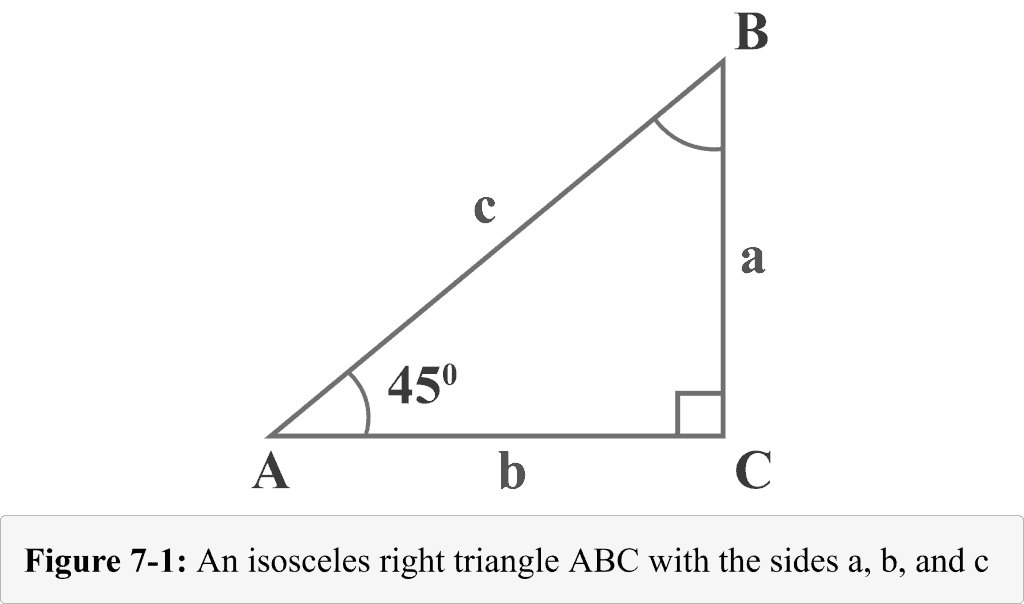
Looking at diagram seven-i, the measure of angle $A$ is $45^{\circ }$. Since the sum of angles in a triangle is $180^{\circ }$, the measure of angle $B$ would too exist $45^{\circ }$.

As values of trigonometric functions are based on the bending and not on the size of the triangle. For simplicity, we take:

$a = 1$

$b = 1$

In this case the triangle will be isosceles triangle. Nosotros can only decide the hypotenuse using Pythagorean theorem.

$c^{2}=a^{2}+b^{two}$

substitute $a = 1$, $b = 1$ in the formula

$c^{2}=1^{2}+1^{ii}$

$c^{2}= 2$

$c = \sqrt{2}$

The following figure seven-2 shows that the isosceles triangle has ii equal sides ($a = b = 1$), hypotenuse ($c = \sqrt{2}$), and equal base angles ($45^{\circ }$ and $45^{\circ }$).

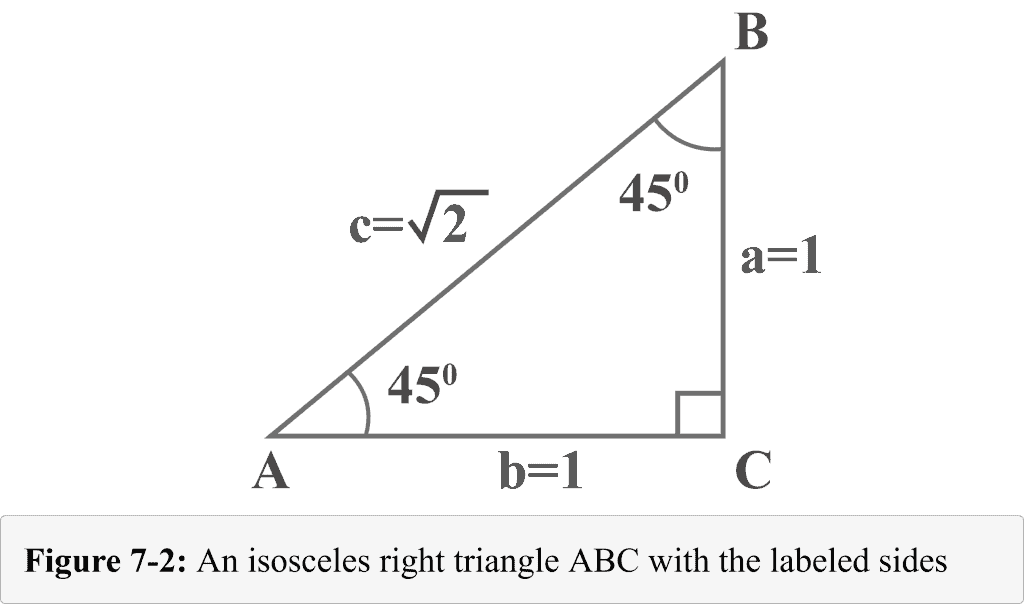
When one thousand ∠ A = 45 ^o:

Nosotros tin can hands make up one's mind the values of trigonometric ratio for $45^{\circ }$.

Looking at diagram vii-two from the perspective of m ∠ A = 45 ^o

Sine function

Southward ine function is the ratio of the opposite side to the hypotenuse.

${\displaystyle \sin 45^{\circ } ={\frac {\mathrm {reverse} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin 45^{\circ } ={\frac {a}{c}}}$

substitute $a = 1$, $c = \sqrt{2}$

${\displaystyle \sin 45^{\circ } ={\frac {1}{\sqrt{2}}}}$

Cosine function

Cos ine function is the ratio of the side by side side to the hypotenuse.

Thus,

${\displaystyle \cos 45^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 45^{\circ } ={\frac {b}{c}}}$

substitute $b = ane$, $c = \sqrt{two}$

${\displaystyle \cos 45^{\circ } ={\frac {i}{\sqrt{2}}}}$

Tangent function

Tangent function is the ratio of the reverse side to the next side.

Thus,

${\displaystyle \tan 45^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {next} }}}$

${\displaystyle \tan 45^{\circ } ={\frac {a}{b}}}$

substitute $a = 1$, $b = 1$

${\displaystyle \tan 45^{\circ } ={\frac {1}{1}}}$

Cosecant part

Cosecant function is the ratio of the hypotenuse to the contrary side.

Thus,

${\displaystyle \csc 45^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 45^{\circ } ={\frac {c}{a}}}$

substitute $c = \sqrt{2}$, $a = 1$

${\displaystyle \csc 45^{\circ } ={\frac { \sqrt{2}}{1}}}$

$\csc 45^{\circ } = \sqrt{2}$

Secant function

Secant office is the ratio of the hypotenuse to the adjacent side.

Thus,

${\displaystyle \sec 45^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {next} }}}$

${\displaystyle \sec 45^{\circ } ={\frac {c}{b}}}$

substitute $c = \sqrt{2}$, $b = 1$

${\displaystyle \sec 45^{\circ } ={\frac { \sqrt{2}}{one}}}$

$\sec 45^{\circ } = \sqrt{2}$

Cotangent office

Cotangent function is the ratio of the adjacent side to the reverse side.

Thus,

${\displaystyle \cot 45^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {reverse} }}}$

${\displaystyle \cot 45^{\circ } ={\frac {b}{a}}}$

substitute $b = 1$, $a = 1$

${\displaystyle \cot 45^{\circ } ={\frac {1}{1}}}$

Case ii:

Special angles xxx^o and 60^o (from a xxx^o – lx^o – 90^o triangle)

The following figure 7-3 represents an equilateral triangle with sides $a = ii$, $b = two$, and $c =ii$. Since equilateral triangle has congruent angles and the measure of angles in a triangle is $180^{\circ }$, each angle measures $60^{\circ }$.

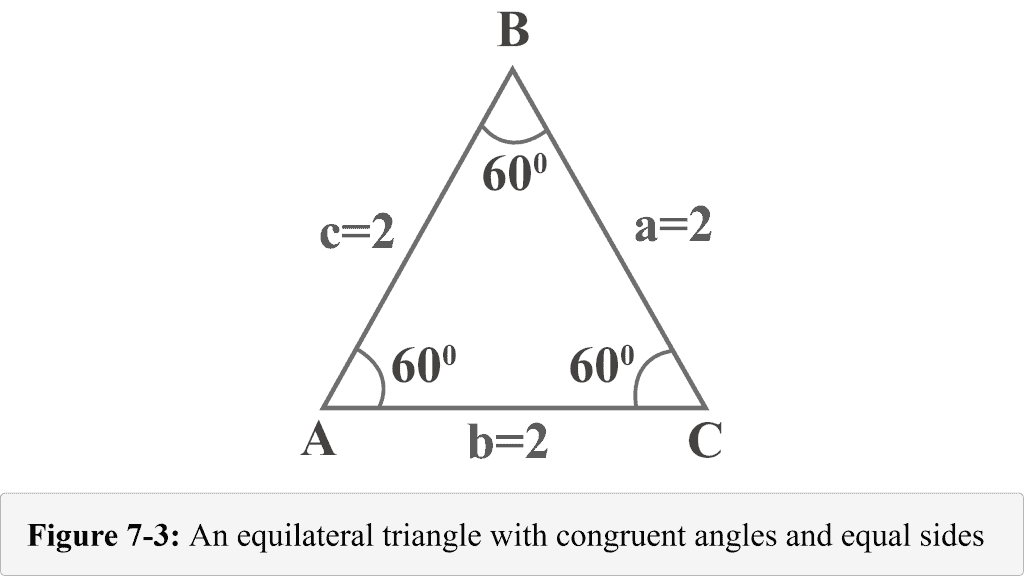
Let usa draw an distance from the vertex $B$. The altitude separates an equilateral triangle into ii coinciding right triangles. In Figure vii-4, ${\displaystyle {\overline {BD}}}$ is altitude, $ΔABD\:≅\:ΔCBD$, $∠BDA$ is a correct angle, $one thousand∠A=60^{\circ }$, and $grand∠ABD=30^{\circ }$.

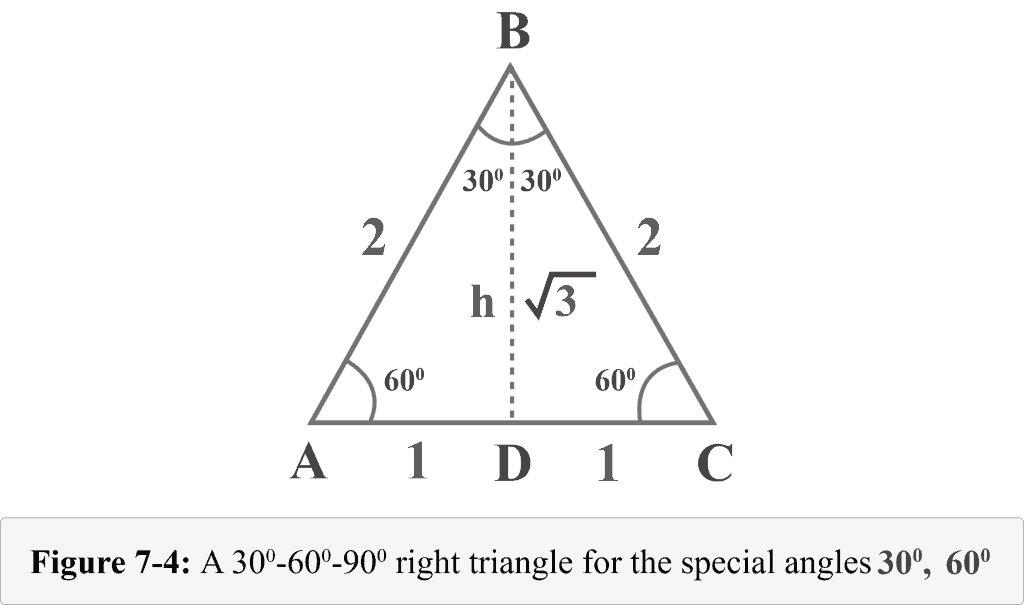
We tin make up one's mind the height h of these triangles by the Pythagorean theorem.

$(AB)^{2}=(BD)^{2}+(AD)^{2}$

$(BD)^{2}=(AB)^{2} – (AD)^{2}$

Substitute $(BD) = h$, $AB = two$, and $Advert = one$ in the formula

$h^{ii}=(2)^{2} – (1)^{2}$

$h^{two}= 3$

$h = \sqrt{3}$

As the altitude $h$ splits the equilateral triangle into two congruent 30^o– 60^o – 90^o triangles. Let united states of america knock out ane of those correct triangles, allow suppose $ABD$, and determine the values of trigonometric ratio for $xxx^{\circ }$ and $lx^{\circ }$.

When g ∠ B = 30 ^o:

The following Figure vii-5 represents the right-angled triangle from the perspective of the special angle $B = 30^{\circ }$.

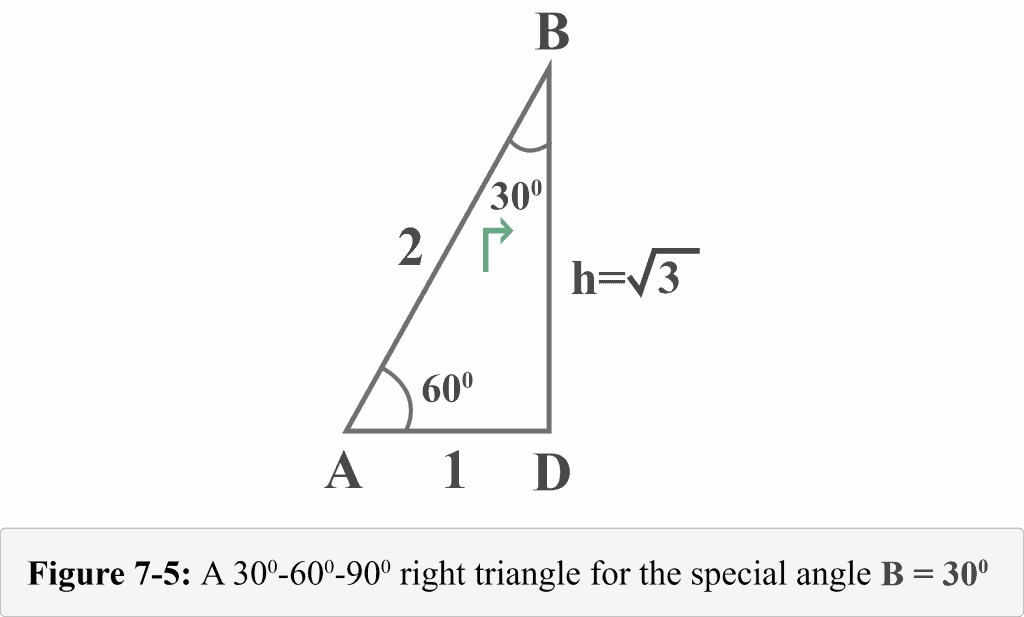
At present, we can easily determine the values of trigonometric ratio for $B = 30^{\circ }$.

Looking at the diagram 7-five from the perspective of grand ∠ B = 30 ^o

Sine function

${\displaystyle \sin 30^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin 30^{\circ } ={\frac {AD}{AB}}}$

substituting $Advertizement = 1$ and $AB = 2$

${\displaystyle \sin 30^{\circ } ={\frac {1}{2}}}$

Cosine office

${\displaystyle \cos 30^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 30^{\circ } ={\frac {BD}{AB}}}$

substituting $BD = \sqrt{three}$ and $AB = 2$

${\displaystyle \cos xxx^{\circ } ={\frac {\sqrt{3}}{2}}}$

Tangent part

${\displaystyle \tan 30^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

${\displaystyle \tan 30^{\circ } ={\frac {AD}{BD}}}$

substituting $AD = i$ and $BD = \sqrt{3}$

${\displaystyle \tan 30^{\circ } ={\frac {i}{\sqrt{3}}}}$

Cosecant function

${\displaystyle \csc thirty^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 30^{\circ } ={\frac {AB}{AD}}}$

substituting $AB = 2$ and $Advertizement = 1$

${\displaystyle \csc 30^{\circ } ={\frac {2}{ane}}}$

Secant function

${\displaystyle \sec 30^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {side by side} }}}$

${\displaystyle \sec 30^{\circ } ={\frac {AB}{BD}}}$

substituting $AB = two$ and $BD = \sqrt{three}$

${\displaystyle \sec 30^{\circ } ={\frac {ii}{\sqrt{iii}}}}$

Cotangent function

${\displaystyle \cot xxx^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

${\displaystyle \cot 30^{\circ } ={\frac {BD}{AD}}}$

substituting $BD = \sqrt{iii}$ and $AD = 1$

${\displaystyle \cot 30^{\circ } ={\frac {\sqrt{three}}{one}}}$

$\cot 30^{\circ } = \sqrt{iii}$

When m ∠ A = 60 ^o:

The following Figure 7-half dozen represents the correct-angled triangle from the perspective of the special bending $A = 60^{\circ }$.

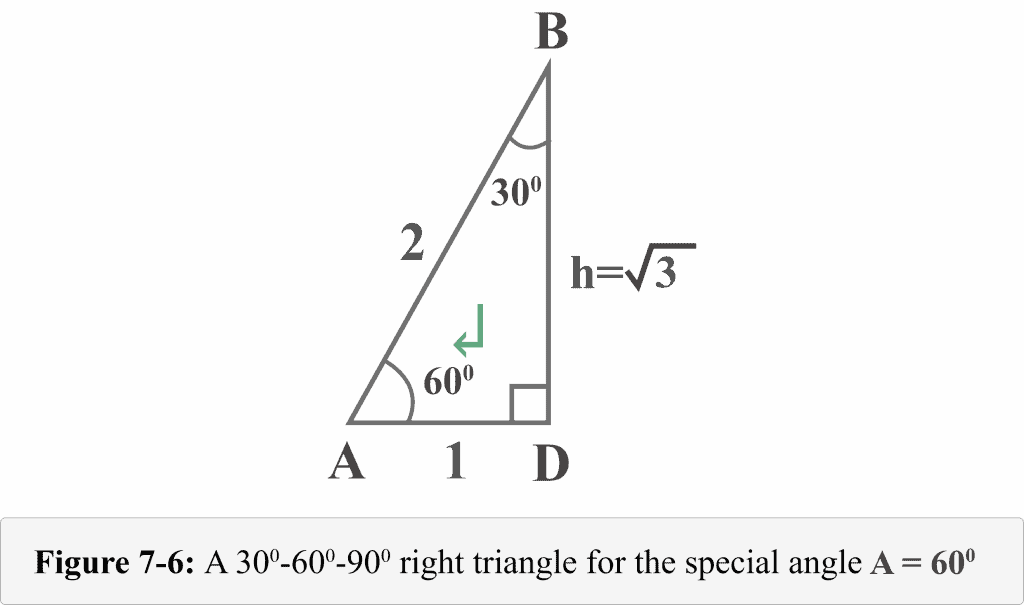
Now, nosotros can easily determine the values of trigonometric ratio for $A = 60^{\circ }$.

Looking at the diagram 7-half dozen from the perspective of grand ∠ A = 60^o

Sine function

${\displaystyle \sin lx^{\circ } ={\frac {\mathrm {contrary} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin threescore^{\circ } ={\frac {BD}{AB}}}$

substituting $BD = \sqrt{3}$ and $AB = ii$

${\displaystyle \sin 60^{\circ } ={\frac {\sqrt{3}}{two}}}$

Cosine part

${\displaystyle \cos 60^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 60^{\circ } ={\frac {Advertising}{AB}}}$

substituting $Ad = i$ and $AB = two$

${\displaystyle \cos sixty^{\circ } ={\frac {ane}{2}}}$

Tangent function

${\displaystyle \tan sixty^{\circ } ={\frac {\mathrm {contrary} }{\mathrm {side by side} }}}$

${\displaystyle \tan sixty^{\circ } ={\frac {BD}{AD}}}$

substituting $BD = \sqrt{3}$ and $Advertizing = 1$

${\displaystyle \tan 60^{\circ } ={\frac {\sqrt{3}}{1}}}$

$\tan 60^{\circ } = \sqrt{3}$

Cosecant function

${\displaystyle \csc threescore^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 60^{\circ } ={\frac {AB}{BD}}}$

substituting and $AB = 2$ and $BD = \sqrt{3}$

${\displaystyle \csc 60^{\circ } ={\frac {ii}{\sqrt{three}}}}$

Secant part

${\displaystyle \sec 60^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {agjacent} }}}$

${\displaystyle \sec 60^{\circ } ={\frac {AB}{Ad}}}$

substituting $AB = two$ and $AD = 1$

Cotangent function

${\displaystyle \cot threescore^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

${\displaystyle \cot 60^{\circ } ={\frac {Ad}{BD}}}$

substituting $Advertizing = 1$ and $BD = \sqrt{3}$

${\displaystyle \cot 60^{\circ } ={\frac {1}{\sqrt{3}}}}$

Here is the complete chart for the values of trigonometric ratio for the special angles $xxx^{\circ }$, $45^{\circ }$, and $60^{\circ }$.

	$xxx^{\circ }$	$45^{\circ }$	$60^{\circ }$
$\sin$	${\frac {i}{two}}$	${\frac { 1}{\sqrt{two}}}$	${\frac {\sqrt{iii}}{2}}$
$\cos$	${\frac {\sqrt{3}}{ii}}$	${\frac { 1}{\sqrt{ii}}}$	${\frac {i}{ii}}$
$\tan$	${\frac { 1}{\sqrt{three}}}$	$1$	$\sqrt{3}$
$\csc$	$2$	$\sqrt{two}$	${\frac { 2}{\sqrt{3}}}$
$\sec$	${\frac { 2}{\sqrt{3}}}$	$\sqrt{ii}$	$2$
$\cot$	$\sqrt{three}$	$1$	${\frac { 1}{\sqrt{3}}}$

Table vii.1

Example $1$

Find the exact value of the following trigonometric expression without using a reckoner.

$\tan 30^{\circ } – \cot 60^{\circ } + \tan 45^{\circ }$

Solution:

$\tan 30^{\circ } – \cot 60^{\circ } + \tan 45^{\circ }$

Using the tabular array,

substitute ${\displaystyle \tan xxx^{\circ } ={\frac {one}{\sqrt{three}}}}$, ${\displaystyle \cot threescore^{\circ } ={\frac {i}{\sqrt{iii}}}}$, $\tan 45^{\circ }=1$

= ${\frac { 1}{\sqrt{3}}} – {\frac { 1}{\sqrt{3}}} + 1$

= $0 + 1$

= $one$

Example $2$

Find the verbal value of the post-obit trigonometric expression.

$4\csc 30^{\circ } + four\tan 45^{\circ } + 7\sec threescore^{\circ }$

Solution:

$4\csc 30^{\circ } + 4\tan 45^{\circ } + 7\sec lx^{\circ }$

= $4 (two) + four (1) + seven (ii)$

= $viii + iv + fourteen$

= $26$

Case $3$

Find the exact value of the following trigonometric expression.

$2\:\left(\sin\:30^{\circ }\right)^two+\:three\:\left(\cos\:xxx^{\circ }\correct)^2\:+\:6\:\left(\tan\:xxx^{\circ }\right)^ii+\:2\:\left(\cot\:45^{\circ }\correct)^ii$

= $2\left(\frac{ane}{ii}\right)^two\:+\:three\:\left(\frac{\sqrt{3}}{2}\right)^2\:+\:vi\:\left(\frac{1}{\sqrt{3}}\right)^2\:+two$

= $2\left(\frac{i}{4}\right)+\:iii\:\left(\frac{iii}{four}\right)\:+\:six\:\left(\frac{1}{3}\right)\:+two$

= $\frac{1}{2}+\frac{9}{four}+two+2$

= $\frac{1}{2}+\frac{ix}{4}+4$

= $\frac{27}{4}$